Gases: Speed Distribution and Effusion
- Sourish W.
- Apr 21, 2020
- 3 min read
We arent done with gases just yet. Today we are reviewing more concepts about gases and kinetic molecular theory. We will look at distribution of velocities for gases and effusion rates. Lets move forward!
In a sample of gas, the molecules are moving with a certain velocity. However, the ranges for the speed of these molecules are widely varying, however the average velocity is dependent upon the temperature of the overall sample. At a given temperature, all gases have the same average kinetic energy.
The molecular speed distribution in a sample of gas, plotting frequency of molecules against their speeds is known as a Maxwell-Boltzmann distribution. A key concept to keep clear is that Gases at higher temperatures will have greater average speeds, however, the distribution of the molecular speeds will be more spread out. Gas samples with larger temperatures have molecular speed distributions that have a greater spread and lower height than lower temperatures, yet the average speed is higher.

Gases with smaller masses have greater velocities than those that have greater masses at the same temperature.
(Cross curriculum knowlege from the energy unit of physics! Lets use the physics equation KE = 1/2 mv^2. We can see that mass and velocity are inversely square root proportional. Smaller masses indicate greater velocities to keep kinetic energy constant at a given temperature. Thus, we can justify the fact above that smaller molecules have greater velocities, as to keep kinetic energy constant at a given temperature, velocity must compensate by increasing if mass is smaller:)
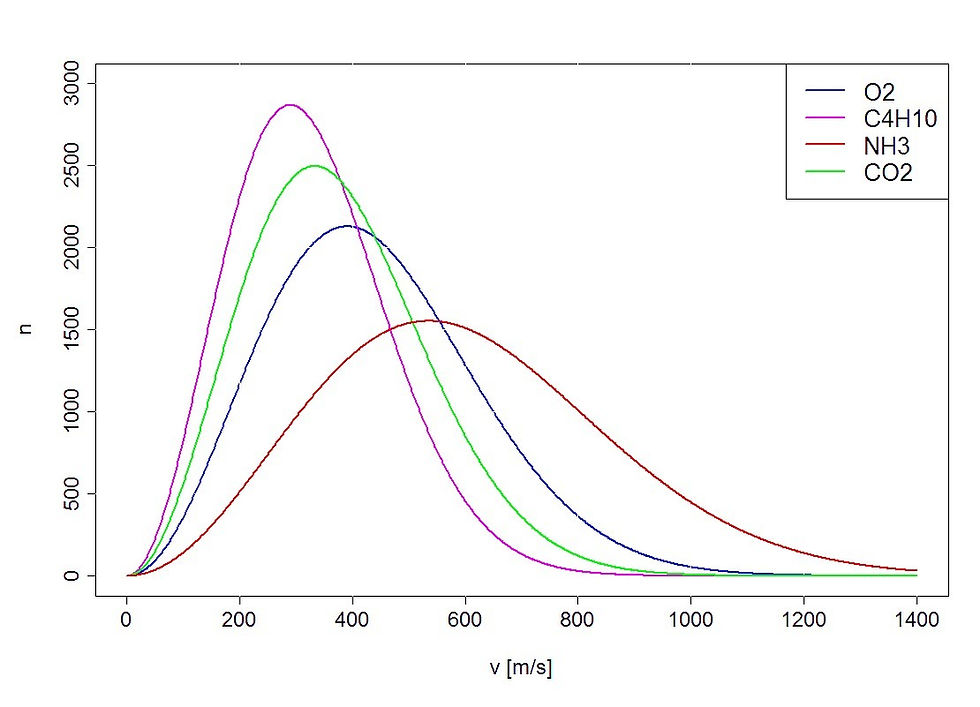
As you can see, the lighter molecules have greater average velocities compared to heavier molecules. Furthermore, we can see that a greater average velocity corresponds with a wider distribution of velocities and a shorter height. This is just as we explained.
The root mean square velocity equation of a sample of gas particles can be derived from
KE = 1/2mu^2 and KE =3/2 RT, and can be calculated with the following formula:
Urms = (3RT/M)^0.5.
The R represents universal gas constant, this time with value 8.314 J/molK
The T represents temperature in Kelvin
The M represents the molecular mass of the particles.
Now, lets talk about rate of effusion. Rate of effusion is the rate at which gas particles of a certain molecule can escape through a pinhole sized hole.
Effusion rate is directly proportional with the average speed of the molecules, thus molecules with greater speeds have greater rates of effusion.
The proportion between the effusion rate of two gases is equal to the proportion between their average molecular velocities. These themselves are related to their molar masses, and as common terms can be canceled, and variables are flipped and rearranged we are finally left with the following
(Rate of Effusion of Particle A) Urms A (1/Ma)^0.5
--------------------------------------- = --------- = ------------- = (Mb/Ma)^0.5
(Rate of Effusion of Particle B) Urms B (1/Mb)^0.5
Thus we can see that the ratio between rates of effusion of different gases is related to their masses in quite a nice way. We can thus see that given two different gases in the same container, the rate of effusion of the smaller mass would be larger than that of the larger mass. We already justified this through proportionality with average speeds, but this ratio can help quantitatively with calculations.
This topic can be confusing, so be sure to let me know if there are any questions about anything gas related in the comments. Please check out the other articles on this website. Happy Studying!



Comments